HW 7 -- Symbolic and continuous planning

This week's Colab notebook can be found here: Colab Notebook (Click Me!)

1) Warming up with Pyperplan§

In this homework, we will be using a Python PDDL planner called pyperplan. Let's warm up by using pyperplan to solve a given blocks PDDL problem.

1.1) Let's Make a Plan§

Use run_planning to find a plan for the blocks problem defined at the top of the colab file (BLOCKS_DOMAIN, BLOCKS_PROBLEM).

The run_planning function takes in a PDDL domain string, a PDDL problem string, the name of a search algorithm, and the name of a heuristic (if the search algorithm is informed) or a customized heuristic class. It then uses the Python planning library pyperplan to find a plan.

The plan returned by run_planning is a list of pyperplan Operators. You should not need to manipulate these data structures directly in this homework, but if you are curious about the definition, see here.

The search algs available in pyperplan are: astar, wastar, gbf, bfs, ehs, ids, sat. The heuristics available in pyperplan are: blind, hadd, hmax, hsa, hff, lmcut, landmark.

For this question, use the astar search algorithm with the hadd heuristic.

For reference, our solution is 2 line(s) of code.

def planning_warmup(): '''Use run_planning to find a plan for the blocks problem defined at the top of the colab file (BLOCKS_DOMAIN, BLOCKS_PROBLEM). Use the astar search algorithm with the hadd heuristic. Returns: plan: A list of actions; each action is a pyperplan Operator. ''' raise NotImplementedError("Implement me!")

1.2) Fill in the Blanks§

You've received PDDL domain and problem strings from your boss and you need to make a plan, pronto! Unfortunately, some of the PDDL is missing.

Here's what you know. What you're trying to model is a newspaper delivery robot. The robot starts out at a "home base" where there are papers that it can pick up. The robot can hold arbitrarily many papers at once. It can then move around to different locations and deliver papers.

Not all locations want a paper -- the goal is to satisfy all the locations that do want a paper.

You also know:

• There are 6 locations in addition to 1 for the homebase. Locations 1, 2, 3, and 4 want paper; locations 5 and 6 do not.
• There are 8 papers at the homebase.
• The robot is initially at the homebase with no papers packed.

Use this description to complete the PDDL domain and problem. You can assume the PDDL planner will find the optimal solution.

If you are running into issues writing or debugging the PDDL you can check out this online PDDL editor, which comes with a built-in planner: editor.planning.domains. To use the editor, you can create two files, one for the domain and one for the problem. You can then click "Solve" at the top to use the built-in planner.

For a general reference on PDDL, check out planning.wiki. Note that the PDDL features supported by pyperplan are very limited: types and constants are supported, but that's about it. If you want to make a domain that involves more advanced features, you can try the built-in planner at editor.planning.domains, or you can use any other PDDL planner of your choosing.

Debugging PDDL can be painful. The online editor at editor.planning.domains is helpful: pay attention to the syntax highlighting and to the line numbers in error messages that result from trying to Solve. To debug, you can also comment out multiple lines of your files by highlighting and using command+/. Common issues to watch out for include:

• A predicate is not defined in the domain file
• A variable name does not start with a question mark
• An illegal character is used (we recommended sticking with alphanumeric characters, dashes, or underscores; and don't start any names with numbers)
• An operator is missing a parameter (in general, the parameters should be exactly the variables that are used anywhere in the operator's preconditions or effects)
• An operator is missing a necessary precondition or effect
• Using negated preconditions, which are not allowed in basic Strips

If you get stuck debugging your PDDL file for more than 10-15 min, please reach out and we'll help!

For reference, our solution is 89 line(s) of code.

def pddl_warmup(): '''Creates a PDDL domain and problem strs for newspaper delivery (uses TYPING). Returns: domain: str problem: str ''' domain_str = '''(define (domain newspapers) (:requirements :strips :typing) (:types loc paper) (:predicates (isHomeBase ?loc - loc) ; TODO: Add missing predicates! ) (:action pick-up :parameters () ; TODO: Add missing parameters! :precondition (and (at ?loc) (isHomeBase ?loc) (unpacked ?paper) ) :effect (and (not (unpacked ?paper)) (carrying ?paper) ) ) (:action move :parameters (?from - loc ?to - loc) :precondition (and (at ?from) ) :effect (and (not (at ?from)) (at ?to) ) ) (:action deliver :parameters (?paper - paper ?loc - loc) :precondition (and ; TODO: Add missing preconditions! ) :effect (and ; TODO: Add missing effects! ) ) )''' problem_str = '''(define (problem newspapers1) (:domain newspapers) (:objects loc-0 - loc loc-1 - loc loc-2 - loc loc-3 - loc loc-4 - loc loc-5 - loc loc-6 - loc paper-0 - paper paper-1 - paper paper-2 - paper paper-3 - paper paper-4 - paper paper-5 - paper paper-6 - paper paper-7 - paper ) (:init (at loc-0) (unpacked paper-0) ; TODO: Add missing initial atoms! ) (:goal (and (satisfied loc-1) (satisfied loc-2) (satisfied loc-3) (satisfied loc-4) )) )''' return domain_str, problem_str

2) Planning Heuristics§

Let's now compare different search algorithms and heuristics.

Let's consider two of the search algorithms available in pyperplan: astar, gbf. (gbf stands for greedy-best-first search.)

And the following heuristics: blind, hadd, hmax, hff, lmcut. blind, hmax and lmcut are admissible; hadd and hff are not.

Unfortunately the documentation for pyperplan is limited at the moment, but if you are curious to learn more about its internals, the code is open-sourced on this GitHub repo.

2.1) Comparison§

We have given you a set of blocks planning problem of different complexity BW_BLOCKS_PROBLEM_1 to BW_BLOCKS_PROBLEM_6. You can use the function test_run_planning found in the Colab to test the different combinations of search and heuristic on different problems. There is also a helper function in the Colab to plot the result.

If planning takes more than 30 seconds, just kill the process.

Choose all that apply:

	Problems 1, 2 and 3 are easy (plan in less than 30 seconds) for all the methods.
	Problem 4 is easy (plan in less than 30 seconds) for all the non-blind heuristics.
	Problem 4 is easy (plan in less than 30 seconds) for all the non-blind heuristics, except hmax.
	The blind heuristic is generally hopeless for the bigger problems.
	hadd is generally much better (leads to faster planning) than hmax.
	gbf-lmcut will always find paths of the same length as astar-lmcut (given sufficient time).
	astar-lmcut will always find paths of the same length as astar-hmax (given sufficient time).
	astar-lmcut usually finds paths of the same length as astar-hff (in these problems).
	gbf-hff is a good compromise for planning speed and plan length (in these problems).

2.2) Relax, It's Just Logistics§

Consider the PDDL domain for logistics.

We create a delete-relaxed version of the logistics domain by dropping the negative effects from each operator.

Now we want to compute h^{\textit{ff}} for this initial state and goal

    I = {truck(t), package(p), location(a), location(b),
         location(c), location(d), location(e),
         at(t, a), at(p, c),
         road(a, b), road(b, c), road(c, d), road(a, e),
         road(b, a), road(c, b), road(d, c), road(e, a)}

    G = {at(t, a), at(p, d)}.

1. What are the actions in the relaxed plan that we would extract from the RPG for this problem, using the h^{\textit{ff}} algorithm? Enter the plan as a list of strings; ordering is not important.

   Enter a list of strings, e.g. ["drive-truck(t,a,b)", "unload-truck(p,t,d)"].
   

   

2. What is the value of the heuristic score of the initial state: h^{\textit{ff}}(I)?

   Enter an integer

   

2.3) More Relaxing Fun§

Consider the RPG construction algorithm discussed in class: Lec 7. Mark all that are true.

	If there exists a plan to achieve a goal with a single fact \{\texttt{g}\}, then that fact \texttt{g} must appear in some level of the relaxed planning graph (RPG).
	If there exists a plan to achieve a goal with a single fact \{\texttt{g}\}, then that fact \texttt{g} must appear in the last level of the RPG.
	The last level of the RPG is a superset of all of the facts that could ever be in the state by taking actions from the initial state.
	The initialization (initial state) of the RPG may affect the number of levels in the RPG, but it will not change the final set of facts in the last level of the RPG.
	If a fact \texttt{g} appears in some level of the RPG, then there exists a (non-relaxed) plan to achieve the goal \{\texttt{g}\}.

3) Implementing h^{\textit{ff}}§

In the code below, one of the arguments is a Pyperplan Task instance. Please study these definitions; some of the methods may be useful in writing your code. Note that fact names are strings as are the names of Operator instances. Also, note that most of the attributes are frozenset; if you want to modify them, you can do set(x) to convert a frozenset x to a set.

3.1) Construct Reduced Planning Graph (RPG)§

Given a Pyperplan Task instance and an optional state, return (F_t, A_t), two lists as defined in the RPG pseudo-code from lecture. Note that fact names in the documentation of Task are strings such as '(on a b)' and operator instances are instances of the Operator class; the name of an operator instance is a string such as '(unstack a c)'. If state is None, use task.initial_state.

For reference, our solution is 15 line(s) of code.

def construct_rpg(task, state=None): '''Constructs a Relaxed Planning Graph (RPG) for a given Pyperplan Task and state. If state is None, use the initial_state of the task. Args: task: a Pyperplan Task instance state: a set of facts (can be None) Returns: rpg: A pair (F_sets, A_sets). Note that F_sets has length one longer than A_sets. F_sets is a list and the item in the list at F[t] should be a set of fact names. We expect F_set to be something like "[{'(clear a)', ...}, {'(ontable b)',...}, ...]”. A_sets is a list and the item in the list at A[t] should be a set of operator instance names. We expect A_sets to be something like "[{'(unstack a b)', ...}, {'(stack a b)', ... }, ... ]" ''' raise NotImplementedError("Implement me!")

3.2) Implement h_add§

Given a Pyperplan Task instance and a state (set of facts or None), return h_add(state).

For reference, our solution is 7 line(s) of code.

In addition to all the utilities defined at the top of the Colab notebook, the following functions are available in this question environment: construct_rpg. You may not need to use all of them.

def h_add(task, state=None): '''Computes h_add for a given Pyperplan Task and state. If state is None, use the initial_state of the task. Args: task: a pyperplan Task instance state: a set of facts (can be None) Returns: h: an integer ''' raise NotImplementedError("Implement me!")

3.3) Implement h_ff (OPTIONAL)§

Given a Pyperplan Task and a state (set of facts or None), return h_ff(state).

For reference, our solution is 26 line(s) of code.

In addition to all the utilities defined at the top of the Colab notebook, the following functions are available in this question environment: construct_rpg. You may not need to use all of them.

def h_ff(task, state=None): '''Computes h_ff for a given task and state. If state is None, use the initial_state of the task. Args: task: a Pyperplan Task instance state: a set of facts (can be None) Returns: h: an integer ''' raise NotImplementedError("Implement me!")

4) Robot Motion Planning§

4.1) Configuration Space§

1. True or False: Consider a robot that is a cube with sides 2r and the obstacles are all cuboids (rectangular prisms). If a pure translation path exists in a problem with a point robot and all the dimensions of the obstacles increased by r (each edge is pushed r apart from the center), a path exists in the original problem.

   	True
   	False

   

2. True or False: Consider the same robot and environment. If a pure translation path exists in the original problem. then a pure translation path exists in a problem with a point robot and all the dimensions of the obstacles increased by r (each edge is pushed r apart from the center).

   	True
   	False

   

3. True or False: Consider a robot that is a sphere with radius r and your obstacles are all cuboids (rectangular prisms). If a path exists in a problem with a point robot and all the dimensions of the obstacles increased by r (each edge is pushed r apart from the center), a path exists in the original problem.

   	True
   	False

   

4. True or False: Consider the same (spherical) robot and environment. If a path exists in the original problem, then a path exists in a problem with a point robot and all the dimensions of the obstacles increased by r (each edge is pushed r apart from the center).

   	True
   	False

   

5. True or False: Consider a complicated robot, with many arms, legs, and antennae, but it can be enclosed in a cube of sides 2r and your obstacles are all cuboids (rectangular prisms). If a pure translation path exists in a problem with a point robot and all the dimensions of the obstacles increased by r (each edge is pushed r apart from the center), a path exists in the original problem.

   	True
   	False

   

6. True or False: Consider the same complicated robot and environment. If a pure translation path exists in the original problem, a path exists in a problem with a point robot and all the dimensions of the obstacles increased by r (each edge is pushed r apart from the center).

   	True
   	False

   

7. If your robot has four 6-dof arms and the ability to fly freely, what is the dimension of its configuration space?

   Enter the dimension as an integer.

   

8. If your robot is 2 x 1 rectangle and can move in X, Y in the plane, and there is a single obstacle, which is a 1x1 square, what is the shape of the configuration-space obstacle?

   -- 1x1 rect 2x1 rect 2x2 rect 3x2 rect 2x3 rect 3x3 rect

   

9. If your robot is a 2 x 1 rectangle and can move in X, Y, and \theta (rotation in the plane) and there is a single obstacle, which is a 1x1 square, what is the shape of the configuration-space obstacle?

   -- rectangle in the X,Y space curved figure in the X,Y space rectangle in X,Y,Theta space curved figure in X,Y,Theta space

   

4.2) Planning Algorithms§

For each of the following statements, indicate whether or not it’s true for the standard RRT with linear-interpolation extensions.

1. Mark all that are true.

   	The algorithm is probabilistically complete.
   	The algorithm is correct (if a plan is found, it can be executed safely).
   	The algorithm will tend to put more samples near the start state than most other parts of the space.
   	It is necessary to have a description of the shape of the obstacles in configuration space.
   	It is applicable to robot arms.
   	It is applicable to fixed-wing flying robots.
   	It is applicable to cars.

   

Artie suggests the following new planning method for robots.

• Sample 1000 points randomly in a bounded configuration space. Include the start and goal points.
• Test each pair of points to see whether they can be connected by a collision-free straight line in configuration space.
• Search the resulting graph of connected points for a path from the start to the goal.
• If a path cannot be found, throw away the current samples and graph, and return to the first step. Otherwise, return the path found.

For each of the following statements, indicate whether or not it’s true for Artie's algorithm.

2. Mark all that are true.

   	The algorithm is probabilistically complete.
   	The algorithm is correct (if a plan is found, it can be executed safely).
   	There is a parameter you can tune to take advantage of information you might have about the tightest clearance in the problem.
   	The algorithm will tend to put more samples near the start state than most other parts of the space.
   	It is necessary to have a description of the shape of the obstacles in configuration space.
   	It is applicable to robot arms.
   	It is applicable to fixed-wing flying robots.
   	It is applicable to cars.

   

3. True or False: Is Artie's algorithm the same as the Probabilistic Roadmap (PRM) algorithm that we have seen in the lecture?

   	True
   	False

   

4.3) RRT§

The figure above visualizes an intermediate step in the RRT procedure.

• Configurations A through F are currently in the tree with the edges shown.
• Goal is the goal configuration.
• M is the configuration sampled by the RRT algorithm at this iteration.
• Of the configurations that are in the tree, D is the closest to M.

The figure shows several other configurations. Of these, which configurations and edges will be added to the RRT at this iteration?

1. Enter the set of nodes that will be added to the RRT. Your input should be a list of strings, e.g., ['A', 'B', 'C']

   

2. Enter the set of edges that will be added to the RRT. Your input should be a list of strings. Each string has the form parent_node-child_node, e.g., ['A-B', 'B-C', 'C-D']

   

5) Implementing RRT §

You should understand extend_path before you tackle the RRT implementation.

5.1) Understanding extend_path§

Below we provide pseudocode for the extend_path utility:

1. Input: initial configuration [x_0, y_0]; goal configuration [x_1, y_1].
2. Compute the distance along x and y dimensions: d_x = |x_1 - x_0|, d_y = |y_1 - y_0|.
3. Divide d_x and d_y by max_diff and round up, which yields n_x and n_y.
4. Let n = \max(n_x, n_y). n is the number of steps we need to take from [x_0, y_0] to [x_1, y_1].
5. Do a linear interpolation from [x_0, y_0] to [x_1, y_1], with evenly-spaced n + 1 nodes (inclusive of the initial and goal).
6. Iterate over the generated linearly-interpolated path, check for collision.
7. If a collision is found, return the prefix of the path that does not have any collision.

Make sure you have understood what extend_path is doing. Answer the following questions.

Suppose we have a 2D robot. The initial configuration is [0, 0]. The goal configuration is [2, 4]. The hyperparameter max_diff is set to 0.4. There is an axis-aligned rectangular obstacle from [0.5, 0.9] to [2, 2]. We now run extend_path based on the above arguments.

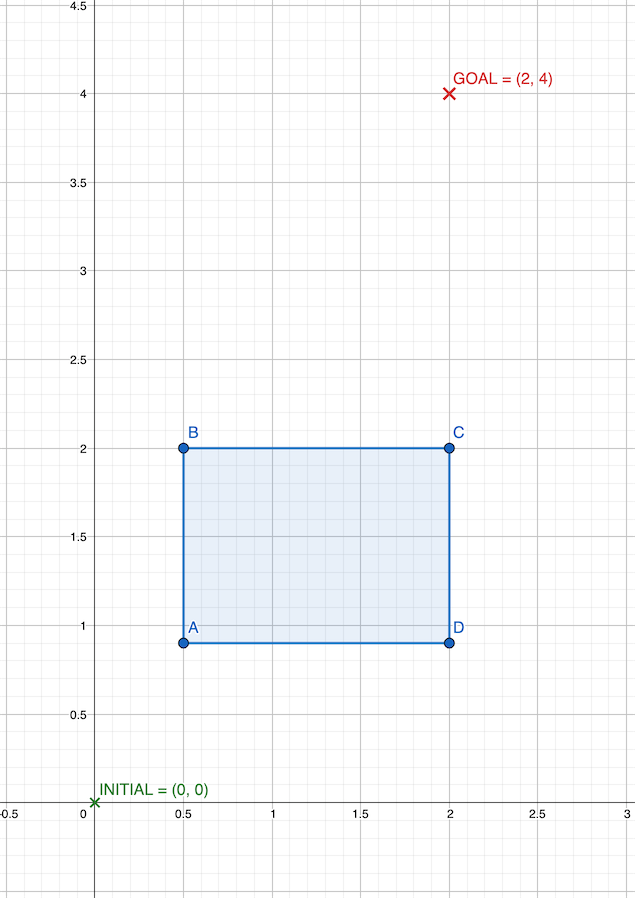
What will be the first return value (i.e. successful)? -- True False

What will be the second return value (i.e. path)? Input your answer as a python list of tuples. For example [(1, 2), (3, 4)]

5.2) Extend Path in a Robot Configuration Space§

In this section, you will implement an important utility for doing motion planning in a continuous space: extend_path. The function takes in a RobotPlanningProblem. It makes a linear interpolation between the start and end configurations in the robot's configuration space.

Its output is a path, that is, a list of robot configurations along the line from start to end. When the start and end cannot be directly connected with a line because of collision, your function should return a "prefix" of the path. In other words, you should try to move along the linearly-interpolated path towards end until you reach some obstacles in the environment.

Take a close look at the docstring of the RobotPlanningProblem class before you implement this function.

Note that:

• Although our test cases are for a two-dimensional configuration [x, y].
  The code for extend_path is written so that it can work for any number of dimensions. Furthermore, the implementation of RRT should also work for any dimension without change.
• Our solution does not use numpy. However, if you are comfortable with numpy, feel free to use it to shorten your implementation.

For reference, our solution is 18 line(s) of code.

def extend_path(problem: RobotPlanningProblem, start: RobotConfig, end: RobotConfig, max_diff: float) -> Tuple[bool, List[RobotConfig]]: '''Construct a linear path in the configuration space from the initial configuration to the goal configuration. Your implementation should have two steps. Step 1, construct a path that is a linear interpolation between `start` and `end`. At each step, the movement along x and along y should be both smaller than or equal to `max_diff`. Step 2: check for collisions. You should iterate over the configurations in the path generated in step 1, if a configuration triggers a collision with an obstacle, your algorithm should return the longest prefix path that does not have any collision. We have implemented this for you. But make sure you read the code and understand how it works. Note that, even though we have separated linear interpolation and collision checking as two separate steps, you can also choose to do them simultaneously in a single for loop. Args: problem: a RobotPlanningProblem instance, used for collision checking. start: a starting RobotConfig. It should be the first element of your return list. end: an ending RobotConfig. It should be the last element of your return list (if succeed). max_diff: the maximum movement in x or y. Returns: successful: a bool value indicating whether we have found a path from the initial configuration to the goal configuration. If a collision happens, you should return False. See the starter code. path: a list of RobotConfig: extending from the initial to the goal configuration. ''' path = [start] # Step 1: Generate a list of robot configurations that connects `start` and `goal`. # Your code only needs to take care of max_diff. We've implemented collision checking in the Step 2 for you. # TODO assert path[-1] == end # Step 2: Collision checking. for i, config in enumerate(path): if problem.collide(config): return False, path[:i] return True, path

5.3) Extend Path Visualization§

We have created a visualization tool for you in colab to visualize the path. You can run the code blocks and they will generate the visualized map and the path.

5.4) RRT§

In this section, you will implement the RRT algorithm we talked about in class to find a path from one configuration to the goal configuration in a 2D environment.

We have implemented some utility classes (RRTNode, RRT) for you, as well as their corresponding visualization tools. You should take a close look at their docstrings before you implement this function. In particular, RRT.__init__, RobotPlanningProblem.sample, RRT.extend, RRT.nearest, RRTNode.backtrace, and extend_path from 2.2 should be helpful. To run in Colab, you will need an implementation of extend_path, if you did not write your own, use the solution in Catsoop.

Hint: Recall that there is a hyperparameter in RRT, which balances how frequently we want to test if the goal configuration can be reached from a node in the current RRT tree. Our suggested value for this hyperparameter is 0.1.

For reference, our solution is 19 line(s) of code.

In addition to all the utilities defined at the top of the Colab notebook, the following functions are available in this question environment: extend_path. You may not need to use all of them.

def rrt(problem: RobotPlanningProblem, max_diff: float, nr_iterations: int = 100, goal_sample_prob: float = 0.1) -> Tuple[List[RobotConfig], RRT]: '''Implement RRT algorithm to compute a path from the initial configuration to the target configuration. Your implementation should returns a list of robot configurations, starting from `problem.initial` and terminating at `problem.goal`. Similar to the definition in extend_path, at each step, the movement along x and along y should be both smaller than or equal to max_diff. You should use the extend_path utility that you just implemented to check whether there is a path from one node to another. Args: problem: an RobotPlanningProblem instance, used for configuration sampling and collision checking. `problem.initial` should be the first element of your return list. `problem.goal` should be the last element of your return list. max_diff: the maximum movement in x or y. nr_iterations: the number of iterations in RRT. goal_sample_prob: at each iteration, with prob p, you should try to construct a path from a node to the goal configuration. Otherwise, you should sample a new configuration and try to construct a path from a node to it. Returns: path: a list of RobotConfig as the trajectory. Return None if we can't find such a path after the specified number of iterations. rrt: an RRT object. The root should be the intial_config. There must also exist another node for goal_config. ''' raise NotImplementedError("Implement me!")

5.5) RRT Visualization§

We have created a visualization tool for you in colab to visualize the RRT tree during your search. You can run the following code blocks and they will generate the visualized the map as well as some lines showing the edges in the RRT.

If you run this cell multiple times, you will see different RRT trees due to different random seeds. You will find that sometimes the tree has very few nodes -- indicating that your RRT algorithm finds a solution very quickly. Sometimes it takes many iterations to find the solution. This suggests that the algorithm is very sensitive to random seeds, which is bad for practical usage. Thus, in practice, we shuold always use improved RRT algorithm variants such as BiRRT (bidirectional RRT).

We recommend you try in your colab notebook to see how the hyperparameter goal_sample_probability will affect the search process. Specifically, try to set that probability to 0.05 or 0.2 and visualize your result.

6) Trajectory Optimizaton §

In this section, you will implement trajectory optimization by minimizing cost functions.

Similar to the robot motion planning section, we will consider \mathbb{R}^2 as both the configuration space and workspace (i.e., the robot is a point). A trajectory optimization problem consists of:

• an initial configuration initial,
• a goal configuration goal, and
• a cost field over \mathbb{R}^2.

The objective of a trajectory optimization problem is to find a trajectory, a path between initial and goal, that minimizes the "cumulative cost" and the trajectory length. Since we are dealing with a continuous state and action space, the "cumulative cost" becomes a path integral over the cost field.

We have provided you with a base class, TrajOpt2DProblem, an abstraction for a general trajectory optimization problem. Further, we have provided two subclasses: the GMTrajOpt2DProblem and the RobotPlanningTrajOpt2DProblem.

• A GMTrajOpt2DProblem is a trajectory optimization problem whose cost field is a mixture of (scaled) Gaussians. The cost field of this problem is similar to the reward field of the FractalProblem you have seen in HW01. In particular, minimizing the negation of a cost field is equivalent to treating the cost field as a reward field and then maximizing cumulative rewards. One of our predefined problems, named gm-2, implements this idea.
• A RobotPlanningTrajOpt2DProblem has a similar setup as RobotPlanningProblem from the previous section. Recall that in a RobotPlanningProblem, the objective is to find a path from initial to goal that avoids some obstacles. To achieve the same objective, a RobotPlanningTrajOpt2DProblem defines its cost field in terms of the obstacles. In particular, at any point p \in \mathbb{R}^2, the cost field is:
  \mathsf{cost}(p) = \max_{o \in \mathsf{obstacles}} \max\left(0, o_\mathsf{radius} + \mathsf{margin} - \| o_\mathsf{center}, p \| \right)
  Here, \mathsf{margin} is a non-negative "safety margin" by which we enlarge each obstacle. The expression \| o_\mathsf{center}, p \| means the Euclidean distance between the obstacle's center and the point p. Therefore, the cost field given above is zero outside of all obstacles' margins and positive otherwise. Further, the costs are higher at points closer to an obstacle's center.

6.1) Numerical Integrator Warmup§

In this problem, you will implement an integrator for a general TrajOpt2DProblem using numerical integration.

Given a TrajOpt2DProblem instance, we will use numerical integration implemented in scipy to approximately compute the path integral over the cost field of the problem. The path integral follows the formula as in AIMA (Section 26.5, P949). Note that since our robot is a point, the inner integration over all points of the robot's body is unnecessary. So our formula will be a simpler version of the one in AIMA.

Given the two endpoints a and b of a line segment, we parameterize the line segment as \tau(t) = (b - a) \cdot t + a for t \in [0, 1]. The path-integral of cost c over the line segment is then:

In words, the path integral of the line segment is the segment's length times the integral of the value of cost field over the line segment.

For this problem, we have implemented most of the code for you. You should only need to fill in the integrand function in the template.

For reference, our solution is 10 line(s) of code.

@dataclasses.dataclass class LineSegCostNumericalIntegrator(LineSegCostIntegrator): '''A generic line segment cost function for any `TrajOpt2DProblem`. ''' problem: TrajOpt2DProblem def __call__(self, lineseg: LineSeg) -> float: a, b = lineseg def integrand(t): '''Evaluate `self.problem`'s cost field at point tau(t) = (b - a) * t + a.''' # YOUR CODE HERE # return 0 seglen = np.linalg.norm(a - b) return scipy.integrate.quad(integrand, 0, 1)[0] * seglen

Note Numerical integration is simple to implement --- especially with an existing package like scipy that already does all the heavy lifting for us. It will work sufficiently well for the small scale problems in this homework. However, In practice, it is almost always better to use closed-form integration instead of numerical integration (if closed-form integration is possible, that is). Therefore, we have provided you with more efficient closed-form integrators for the problems that you will work with. When you implement and run the actual optimization (i.e., traj_opt), we encourage you to use our closed-form integrators since they should be faster and thus easier for you to try out different parameters and settings.

6.2) Trajectory Optimization§

Implement trajectory optimization traj_opt.

The traj_opt function finds a piecewise linear trajectory by performing optimization. It minimizes the sum of two terms J_\textit{cost\_field} and J_\textit{eff} and trades off between the two using \lambda_\textit{eff}:

For our setup:

• J_\textit{eff} = \sum_{p \in \text{segments} } \| p \| is the total length of the trajectory.
• J_\textit{cost\_field} = \sum_{p \in \text{segments}} \texttt{lineseg\_costf}(p) is the sum of the costs returned by lineseg_costf, for all line segments in the piecewise linear trajectory.

We will use the BFGS optimizer implemented in scipy to carry out the minimization.

Here's a rough overview of the algorithm:

1. Create an initial path with num_waypoints number of intermediate points by linearly interpolating between the initial configuration and the goal configuration, This step is similar to extend_path.
2. "Slice" the initial path to contain only the intermediate way points --- these are the parameters of the optimization problem.
3. Add a small random noise perturbation to the initial parameters. (What potential problem are we trying to solve by doing this?)
4. Build the cost functions J_\textit{cost\_field}, J_\textit{eff} and J.
5. Minimize J using scipy.optimize.minimize.
6. Recover the complete trajectory from scipy's optimization result.

Hint: the following numpy functions might be quite handy (though not strictly necessary): np.linspace, np.random.normal, np.stack, np.vstack, np.reshape, np.flatten. In general, leveraging numpy could make your life easier! If you get stuck or unsure how to use these functions, please feel free to reach out and we will be happy to help!

Note Sometimes scipy might return a result with a success=False flag. For our example problems, one common reason of this success=False flag is the loss of accuracy during the optimization. Usually, this is fine and scipy will still return a fairly good solution. However, if you do run into weird results and get stuck, please reach out!

For reference, our solution is 36 line(s) of code.

In addition to all the utilities defined at the top of the Colab notebook, the following functions are available in this question environment: LineSegCostNumericalIntegrator. You may not need to use all of them.

def traj_opt( initial: Point2D, goal: Point2D, lineseg_costf: LineSegCostIntegrator, num_waypoints: int = 5, lambda_eff: float = 10., init_perturb: float = 1e-2 ) -> Tuple[PiecewiseLinearTraj, float, float, bool]: '''Performs trajectory optimization with a given cost function. This function finds a piecewise linear trajectory by performing optimization. It minimizes the sum of a J_cost_field and J_eff (and trades off between the two): J = J_cost_field + lambda_eff * J_eff For our setup: - `J_eff` is the total lengths of all pieces of the trajectory. - `J_cost_field` is the sum of the costs returned by `lineseg_costf`, for all line segments in the piecewise linear trajectory. We will use the BFGS optimizer implemented in scipy to carry out the minimization. Args: initial: the initial point of the trajectory. goal: the goal point of the trajectory. lineseg_costf: a cost function for each line segment in a piecewise linear trajectory. num_waypoints: number of intermediate points for the piecewise linear trajectory (excluding `initial` and `goal`). Must be >= 0. lambda_eff: a weighing factor for J_eff, as in AIMA. init_perturb: this function adds a normally distributed random noise to the initial guess. The noise has zero mean. This parameter controls the variance. Returns: - the optimal piecewise linear trajectory. - the value of J_cost_field of the final trajectory. - the value of J_eff of the final trajectory. - success: whether the optimization converged. See https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.OptimizeResult.html on how to access the optimization result. ''' # Interpolate from initial to goal init_traj = ... # YOUR CODE HERE # Remove initial and goal and flatten the trajectory to shape (num_waypoints*2, ) init_traj_params = ... # YOUR CODE HERE # Add random noise perturbation init_traj_params += np.random.normal(loc=0, scale=init_perturb, size=init_traj_params.shape) def to_complete_trajectory(traj_params): '''Given a set of trajectory parameters of shape (num_waypoints * 2,), return the complete trajectory of shape (num_waypoints+2, 2) that includes the initial and goal.''' return np.vstack([initial, traj_params.reshape(num_waypoints, 2), goal]) def J_cost_field(traj: np.ndarray) -> float: '''Use `lineseg_costf` to compute the total cost of the trajectory.''' # YOUR CODE HERE # def J_eff(traj: np.ndarray) -> float: '''Compute the total length of the trajectory.''' # YOUR CODE HERE # def J(traj_params: np.ndarray) -> float: '''Compute the trajectory cost as: J = J_cost_field + lambda_eff * J_eff''' # YOUR CODE HERE # # Call the optimizer: we have filled in the arguments for you result = scipy.optimize.minimize( J, init_traj_params, method="BFGS", options=dict( gtol=1e-4, maxiter=int(1e6), ), ) # The parameters found by running the optimizer found_traj_params = result.x # Convert parameters back into a complete trajectory traj = ... # YOUR CODE HERE # return traj, J_cost_field(traj), J_eff(traj), result.success

6.3) Trajectory Optimization Visualization§

We have created a visualization tool for you in colab to visualize the result of your traj_opt. You can run the code blocks and they will generate the visualized cost field and the found trajectory.

As you do the visualization, try to:

• Visualize the different problems in get_traj_opt_problems: gm-1,gm-2,robot-planning-1,robot-planning-2,robot-planning-3
• Vary the parameter \lambda_{\textit{eff}} --- are larger or smaller values more likely to produce an obstacle-avoiding path in robot-planning-* problems?

6.4) Tuning \lambda_{\textit{eff}} §

Let us visualize the effect of \lambda_{\textit{eff}}.

For this problem, fix num_waypoints as 6. Then, answer the following questions by visualizing the found trajectories by traj_opt.

1. For robot-planning-1, which of the following setting(s) of \lambda_{\textit{eff}} produced a path without collision?

   	0
   	0.5
   	1.0
   	10.0
   	15.0

   

2. For robot-planning-1, which of the following setting(s) of \lambda_{\textit{eff}} produced a path without collision, but the path is wasteful (i.e., longer than necessary)?

   	0
   	0.5
   	1.0
   	10.0
   	15.0

   

3. For robot-planning-2, which of the following setting(s) of \lambda_{\textit{eff}} produced a path without collision?

   	0
   	0.5
   	1.0
   	10.0
   	15.0

   

6.5) Got Stuck? §

Trajectory optimization some times return solutions that are locally optimal but not globally optimal (with respect to the cost function J).

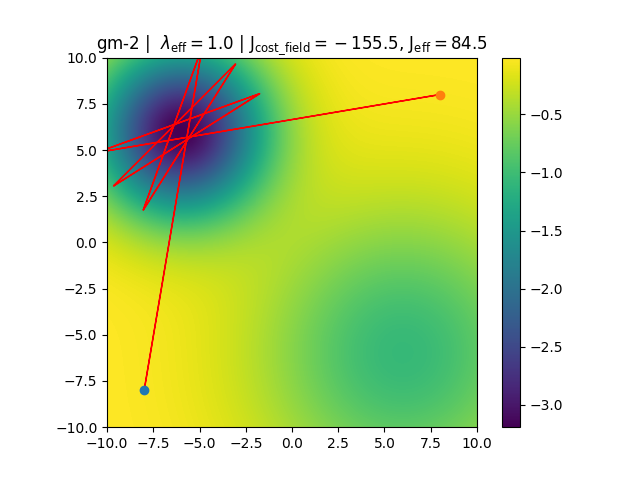
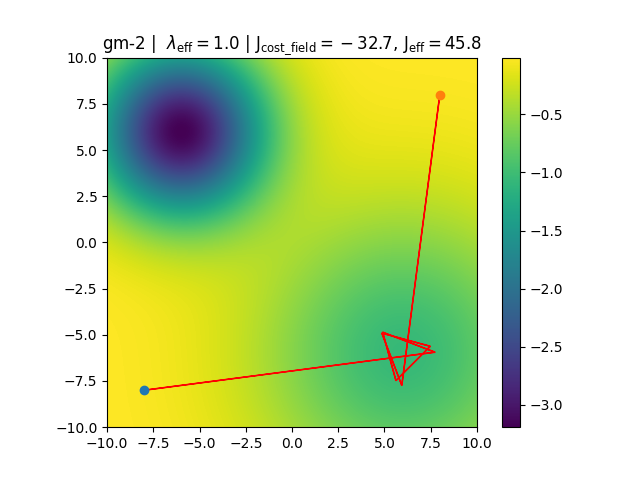
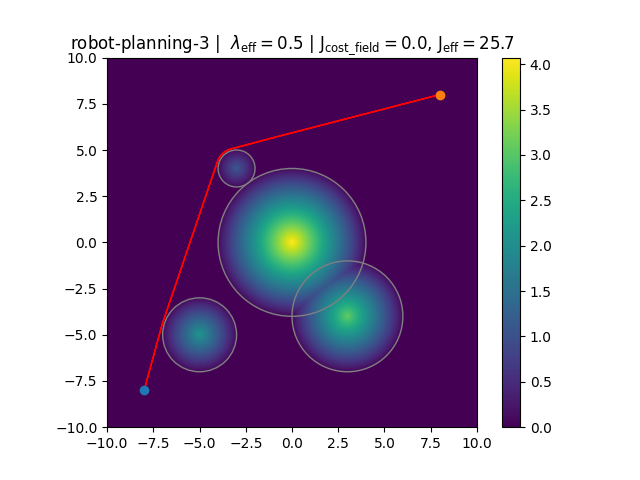
1. Figure A. and B. depict two found trajectories and costs for gm-2. Which of the above trajectories cannot be globally optimal?

   	A
   	B

   

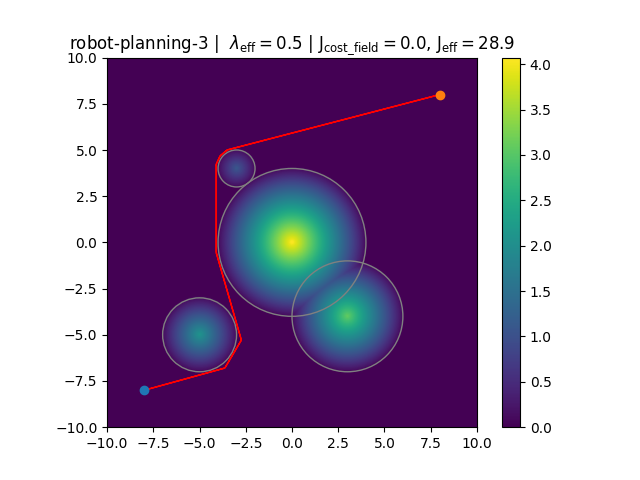
2. Figure C. and D. depict two found trajectories and costs for robot-planning-3. Which of the above trajectories cannot be globally optimal?

   	C
   	D

   

3. Consider the the following found trajectory by traj_opt: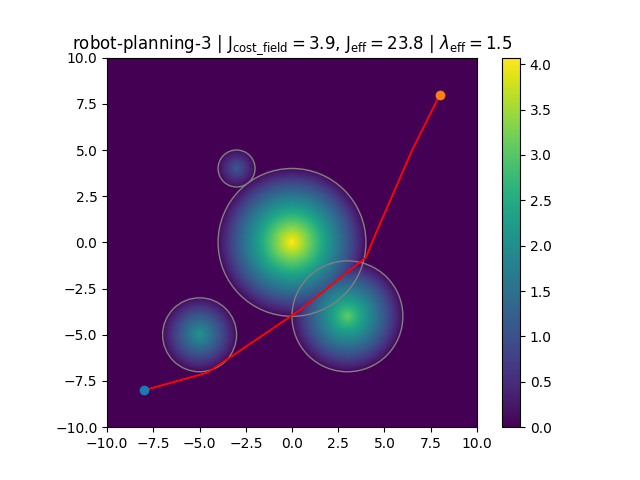

   

Which of the follow changes might allow traj_opt to produce a non-colliding trajectory? Assume that traj_opt always produce a locally (or globally) optimal trajectory.

	Add to the cost function J a positive constant
	Add to the cost function J a negative constant
	Increase \lambda_{\textit{eff}}
	Decrease \lambda_{\textit{eff}}
	Increase the value of margin in RobotPlanningTrajOpt2DProblem
	Decrease the value of margin for RobotPlanningTrajOpt2DProblem

7) Feedback§

1. How many hours did you spend on this homework?

   -- 2 3 4 5 6 7 8 more

   

2. Do you have any comments or suggestions (about the problems or the class)?